A graph is a collection of nodes, called vertices, connected to each other in some fashion by edges. A graph is called connected if it is possible to find a path along edges from every point to every other point.

Below are two graphs:

One on the left is connected, while the one on the right is not connected (there is no path from node 1 to node 3).

An edge of a graph is called a bridge if by removing that edge the graph is no longer connected.

Edge 1-2 in the following graph is a bridge, since by removing it, the graph is no longer connected (no path from node 1 to any other node):

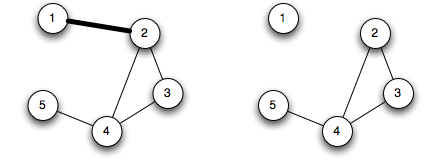
Edge 2-3 however, is not a bridge:

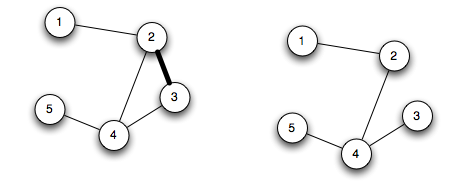
You are tasked with finding the number of edges, in a graph, that are bridges. You will be given 5 connected graphs, and you will output 5 single integers for the number of bridges found in graphs.

The input file is DATA5.txt. First line will contain a single integer N, number of vertices. Vertices will be numbered 1 to N. 1 <= N <= 100 . Second line will contain a single integer M, number of edges. 0 <= M <= 1000 . Followed by M lines, each describing an edge. An edge is described by two integers, separated by a space. All edges are valid. This format will be repeated 5 times (that is, a line after the last edge of the 1st graph, will be a single integer, describing a number of vertices in the 2nd graph).

The output file OUT5.txt will contain 5 lines, a single integer per line -- the number of bridges in the described graph.

6
7
1 2
1 3
1 4
1 5
3 5
6 2
6 1
        

1
        

Explanation of Input:

6 - There are 6 vertices, numbered 1 2 3 4 5 6
7 - There are 7 edges
1 2 - Vertex 1 is connected to vertex 2
1 3 - Vertex 1 is connected to vertex 3
1 4 - Vertex 1 is connected to vertex 4
1 5 - Vertex 1 is connected to vertex 5
3 5 - Vertex 3 is connected to vertex 5
6 2 - Vertex 6 is connected to vertex 2
6 1 - Vertex 6 is connected to vertex 1
        

The sample input would define the following graph:

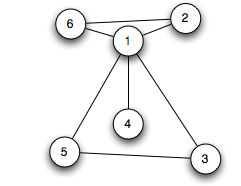
The only bridge is the edge 1-4.